Sitemap
MTBF
MTBF
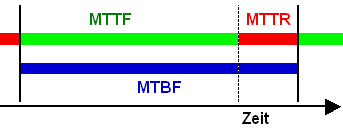
- Mean Time between Failure + MTTF



| Auf
dieser Seite suchen |
|
|
|
|



| Eins hoch |
1. Allgemeines zum Thema MTBF |
Eins runter |

| Eins hoch |
Eins runter |
| Eins hoch |
Eins runter |

 Im Folgenden
werden alle 4
Punkte nacheinander beleuchtet. Die Punkte hängen voneinander ab, d.h.,
wollte man einen Punkt umfassend verstehen, müsste man wenigstens einen
weiteren Punkt vorher verstanden haben. Einen schrittweisen Zugang zum
Thema MTBF
auf eine Weise, die einerseits
erschöpfend ist, andererseits
zu keinem Zeitpunkt Fragen offen lassen muss, hat der Verfasser bislang nicht
gefunden.
Im Folgenden
werden alle 4
Punkte nacheinander beleuchtet. Die Punkte hängen voneinander ab, d.h.,
wollte man einen Punkt umfassend verstehen, müsste man wenigstens einen
weiteren Punkt vorher verstanden haben. Einen schrittweisen Zugang zum
Thema MTBF
auf eine Weise, die einerseits
erschöpfend ist, andererseits
zu keinem Zeitpunkt Fragen offen lassen muss, hat der Verfasser bislang nicht
gefunden. | Eins hoch |
Eins runter |
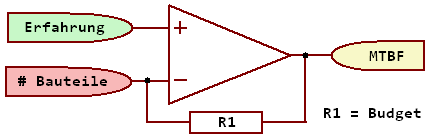
 Es leuchtet
intuitiv ein, dass ein Gerät umso häufiger ausfallen
wird,
je mehr Ausfallmöglichkeiten es hat. Je mehr ein Gerät "kann", desto
mehr Möglichkeiten hat es, auszufallen,
wenn man ansonsten gleiche Bedingungen voraussetzt ("ceteris paribus").
Beispielsweise sind bei einer umfangreichen Produktionsanlage mehr
Störungen zu erwarten als bei einer Handbohrmaschine. Daraus ergibt
sich folgender, grundlegender Sachverhalt:
Es leuchtet
intuitiv ein, dass ein Gerät umso häufiger ausfallen
wird,
je mehr Ausfallmöglichkeiten es hat. Je mehr ein Gerät "kann", desto
mehr Möglichkeiten hat es, auszufallen,
wenn man ansonsten gleiche Bedingungen voraussetzt ("ceteris paribus").
Beispielsweise sind bei einer umfangreichen Produktionsanlage mehr
Störungen zu erwarten als bei einer Handbohrmaschine. Daraus ergibt
sich folgender, grundlegender Sachverhalt:  Populationsgrösse
gebunden sind:
Populationsgrösse
gebunden sind: | Eins hoch |
Eins runter |

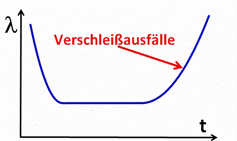
| Am Anfang, wenn die Gerätepopulation in Betrieb genommen wird, ist die Ausfallrate hoch wegen verschiedenen Aspekten, an die man nicht gedacht hat, oder die man falsch eingeschätzt hat. Die damit einher gehenden, so genannten Frühausfälle werden vom Lieferanten (hoffentlich) nach und nach addressiert, sodass die Ausfallrate auf ein akzeptables Niveau sinkt. | 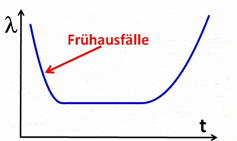 |
| Im
eingeschwungenen Zustand nimmt die Ausfallrate einen niedrigen Wert an.
Warum dieser konstant über die Zeit ist oder sein sollte, wird später
erklärt. Wenn das
Lebensende der Population naht, kommen Alters- und
Verschleisserscheinungen hinzu, was die Ausfallrate wieder nach oben
treibt. |
 |
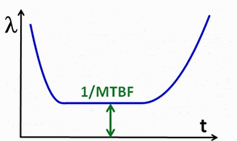 Wollte man MTBF statt 1/MTBF
darstellen, dann müsste man die vertikale Achse umskalieren, und
erhielte eine "umgedrehte" Badewannenkurve. Egal wie man es darstellt, aus den Bildern wird ersichtlich, dass MTBF
und Lebensdauer ganz Unterschiedliches
bedeuten, und vermutlich nichts miteinander zu tun haben. Während
die Lebensdauer eine kalendarische Zeitdauer ist, die der
Benutzer als Gebrauchsdauer erlebt, stellt sich die MTBF
als eine
anschaulich Beschreibung der Wahrscheinlichkeit dar, mit der das Gerät
ausfallen wird. Wiederholung:
Wollte man MTBF statt 1/MTBF
darstellen, dann müsste man die vertikale Achse umskalieren, und
erhielte eine "umgedrehte" Badewannenkurve. Egal wie man es darstellt, aus den Bildern wird ersichtlich, dass MTBF
und Lebensdauer ganz Unterschiedliches
bedeuten, und vermutlich nichts miteinander zu tun haben. Während
die Lebensdauer eine kalendarische Zeitdauer ist, die der
Benutzer als Gebrauchsdauer erlebt, stellt sich die MTBF
als eine
anschaulich Beschreibung der Wahrscheinlichkeit dar, mit der das Gerät
ausfallen wird. Wiederholung:
 Lebensdauer
bisher nicht grundsätzlich verneint wurde. Das obige Beispiel
wurde bewusst so gewählt, dass tatsächlich kein
Zusammenhang bestehen kann.
Lebensdauer
bisher nicht grundsätzlich verneint wurde. Das obige Beispiel
wurde bewusst so gewählt, dass tatsächlich kein
Zusammenhang bestehen kann.  Doch wie werden die Verhältnisse, wenn das
Gerät so umfangreich ist, es
aus so vielen Einzelteilen besteht, dass seine MTBF
niedriger ist als
seine vorgesehene Gebrauchsdauer? Beispiele dafür sind Flugzeuge,
Produktionsanlagen, usw.
Doch wie werden die Verhältnisse, wenn das
Gerät so umfangreich ist, es
aus so vielen Einzelteilen besteht, dass seine MTBF
niedriger ist als
seine vorgesehene Gebrauchsdauer? Beispiele dafür sind Flugzeuge,
Produktionsanlagen, usw. | Eins hoch |
Eins runter |
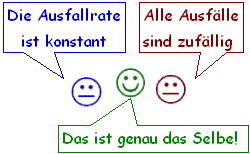 Das Konzept MTBF basiert auf der
Unterscheidung zwischen zufälligen und
systematischen Ausfällen. Berücksichtigt
werden nur zufällige
Ausfälle,
während
systematische Ausfälle ausgeschlossen werden.
Das Konzept MTBF basiert auf der
Unterscheidung zwischen zufälligen und
systematischen Ausfällen. Berücksichtigt
werden nur zufällige
Ausfälle,
während
systematische Ausfälle ausgeschlossen werden. 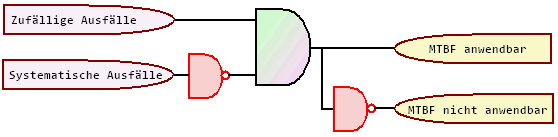
| Eins hoch |
Eins runter |
| Eins hoch |
Eins runter |

 Doch das ist falsch, und leider auch noch
optimistisch (das Ergebnis ist besser als die Wirklichkeit)
Doch das ist falsch, und leider auch noch
optimistisch (das Ergebnis ist besser als die Wirklichkeit) 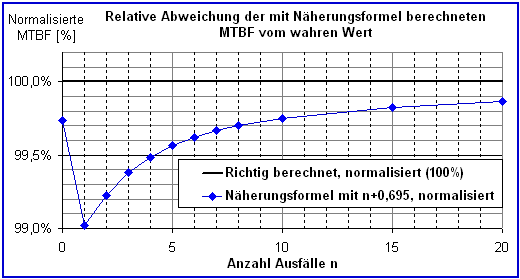
| Eins
hoch |
Eins runter |
| Eins
hoch |
Eins runter |
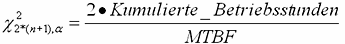
| Eins
hoch |
5. MTBF Berechnung nach Standards |
Ganz hoch |
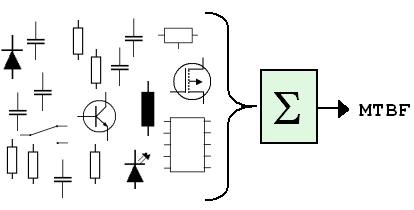 Felddaten sind die
beste Datenquelle, weil diese
Daten unter realen Bedingungen auftretende Ausfälle repräsentieren, und
daher alles beherbergen, was die MTBF
beeinflussen könnte. Labortestdaten sind die zweitbeste Datenquelle,
weil auch sie echte Ausfälle repräsentieren; immerhin werden die Geräte
physikalisch betrieben, und reale Bedingungen können zumindest
angenähert werden.
Felddaten sind die
beste Datenquelle, weil diese
Daten unter realen Bedingungen auftretende Ausfälle repräsentieren, und
daher alles beherbergen, was die MTBF
beeinflussen könnte. Labortestdaten sind die zweitbeste Datenquelle,
weil auch sie echte Ausfälle repräsentieren; immerhin werden die Geräte
physikalisch betrieben, und reale Bedingungen können zumindest
angenähert werden.